The programming area of OpenSCADA system project.
Author: Roman Savochenko
Translated: Maxim Lysenko
1 Introduction
Open SCADA system OpenSCADA belongs to the class of SCADA (Supervisory Control and Data Aquisition) systems. Systems of this class are used as an element of automation of technological processes (ACS TP).
In some cases, SCADA systems can be used at the controller level, combining the functions of the controller with the functions of SCADA systems.
To organize the users' calculations if the area of industrial controllers and SCADA systems the different programming languages are used. In the case of controllers the low-level languages (assemblers) are often used, but in recent years the high-level languages (C, Pascal and others) are used more and more, as well as formal languages (block scheme, relay scheme, logic scheme and others). In the case of SCADA systems the calculations most of all are provided by the high-level programming languages and formal languages.
Providing the user programming area by any software system in general is an important indicator of quality and maturity ùof the system.
This project is provided to develop the programming area of the OpenSCADA system.
2 Purpose
Functionally the development is intended to create in OpenSCADA system the components of programming are with which you can implement various calculations and control algorithms within the OpenSCADA system.
Operating appointment of the development is:
- expansion of the scope of the OpenSCADA system by increasing the flexibility of the programming area;
- reduce the labor costs for the creation of mathematical models of technological processes;
- possibility to create large models using the elements of previous models.
3 Requirements
3.1 Architectural requirements for the programming area
Under the architectural requirements it is meant with what structure the development should follow.
The peculiarity of the OpenSCADA system architecture imposes the relevant requirements to the development's architecture. Thus, taking into account the modularity, flexibility and scalability of the OpenSCADA system, it is necessary to ensure these characteristics with this development.
With this purpose the programming area architecturally can be divided into three parts:
- declaring objects in the OpenSCADA system kernel;
- function's objects libraries functions (API of the object model of OpenSCADA);
- computing controllers and other computing nodes of the system.
Objects of functions should contain only the structure of functions' parameters and computation's algorithm. The real values must be passed to the functions' object in the form of values' frame by different computation controllers and nodes.
Declaring objects must be contained in the OpenSCADA kernel to provide the access to all components of the programming area.
Values' frames that pass to the functions' objects in during the calculations should be stored in the nodes that require the calculations. These nodes can be:
- calculation controllers;
- visualization area;
- logic level of the parameters;
- other calculation nodes.
3.2 General requirements
Lets show the requirements for the programming area, based on the architectural requirements, which require the separation of the programming area into three parts.
The OpenSCADA system core must provide:
- storage of the declaring structures: functions' objects, functions' parameters and functions' values frame;
- binding the values frame with the function;
- support of the parameters of the standard types of OpenSCADA: integer, real, boolean and string;
- possibility of testing the functions for the specified input data;
Within the project it must be implemented the following function libraries and calculation controllers:
- module(s) of the static functions' libraries;
- calculator module on the high level programming language and the module of the functions' libraries on the high-level language (concurrently);
- calculator module on the language of the blocks.
Module(s) of the static functions' libraries must provide:
- formation of the library of standard mathematical functions;
- formation of the library of compatibility functions with the SCADA Complex1 of company NIP "DIYA";
- service of the system commands of start and stop the module to provide the support for automatic update the module of libraries.
Module of the calculator on the high-level programming language and the module of the functions' libraries on this language should provide:
- configuration of the controllers of this type with the ability to set the period of calculation and the number of calculations in one cycle;
- simple parameters' types to access the calculator's data from the system;
- creation of the parameters of the calculating function of the controller of subsystem "DAQ" (tables of data);
- creation of the program for calculating for the controller of "DAQ" subsystem;
- support of the addressing to the attributes of the parameters of the controller of "DAQ" subsystem from the calculating program;
- formation of functions' libraries of the user;
- formation of the functions by the user;
- editing the parameters of functions with anticipation of the functionsý user (values frames) about the change of structure, ie without interrupting the calculation and blocking the possibility of modification;
- creation the function's program.
Module of the calculator on the block's language must provide:
- configuration of the controllers of this type with the ability to set the period of calculation and the number of calculations in one cycle;
- simple types of the parameters of the controller of "DAQ" subsystem for access to the calculator's data from the system;
- building blocks of the block scheme;
- blocks' binding with each other and with the attributes of the parameters.
3.3 Requirements to the high-level programming language
To implementation of the calculator module on the high-level programming language and the module of functions' libraries on the same language you must use the grammar of one of the known high-level languages.
Program in the chosen language must be compiled into the code of the internal virtual machine. The main requirements for the virtual machine are: high reliability and performance. To get the high reliability of the virtual machine it must contain mechanisms for accounting and limiting the calculation time.
It is obligatory to be implemented the following features of programming language:
- support of the major operations;
- support of the complex expressions with the priorities of operations;
- Support of the brackets for the separation of foreground sections;
- support of the basic data types of OpenSCADA: integer, real, boolean and string;
- support of the lightweight scheme of the types' cast;
- support of the conditional statements, among them: if, for, while;
- support of the brackets for grouping the expressions;
- support of the call of functions, including built-in and external (from the object model OM).
3.4 Requirements to the developing block programming language
Language of the block schemes can be based on the available functions of functions' libraries of the object model of OpenSCADA. Each block may be associated with the function and form the structure of values in accordance with the structure of function. Each block must ensure the inclusion and exclusion from the processing action, not stopping the calculation of the whole scheme.
To tie(link) the blocks with one another the support for the following types of links must be provided:
- interblock - connecting the input of the one block to the output of the another one, as well as the output of one block to the input of another;
- long interblock - the union of blocks of different controllers in the module;
- factor - the transformation of input into the constant, all inputs/outputs by default are initiated as constants;
- external attribute of the parameter.
Links must maintain their "hot" in the process of calculating setting.
4 Engineering
4.1 Problem definition
Any complex software system should contain a programming area. The presence of such an area significantly enhances the flexibility of the system and, consequently, the scope of its application. Programming area, which is used in such software systems, may be based on different programming languages. However, the most commonly used languages, endowed with a high level of formalism, for example, languages of blocks (block schemes, logical schemes, relay schemes and others). But, together with them the high-level languages such as C and C++ in its simplified reincarnation: Java and JavaScript are frequently used. Sometimes the languages of the logical output: Prolog and Lisp are also used.
OpenSCADA system is developed as the flexible and highly scalable SCADA system, so creating of own programming area is an important task. The main purpose of creating the user programming area is to provide the OpenSCADA system with the flexible and powerful programming mechanism.
In addition, a programming area is designed to provide an opportunity for creation of:
- algorithms for technological process control;
- models of technological, chemical, physical and other processes, as well as for the implementation of adaptive control mechanisms within the models;
- user programs to control the internal functions of the OpenSCADA system and its subsystems and modules;
- ãèáêîãî ôîðìèðîâàíèÿ ñòðóêòóð ïàðàìåòðîâ íà óðîâíå ïîëüçîâàòåëÿ (ëîãè÷åñêèé óðîâåíü);
- additional calculations.
4.2 The function's object as the key element of the programming area
The key element of the programming area as an object the function is selected, where the function is defined as the container that contains the data structures (parameters) and an algorithm for their calculation. The parameters can be both inputs and outputs. This somewhat simplified object structure that combines the object with the mechanism, thus simplifying the initial perception and the creation of the programming area. In addition, this choice does not exclude the possibility of creation of the full-fledged object model (OM) in the future.
That is, we have an elementary module - Figure 1.
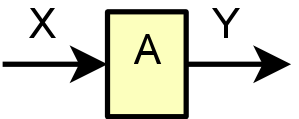
Fig. 1. Function
Where:
Y – set of outputs;
A – inputs processing algorithm.
As you can see, this module does not contain the states, because it does not store any values of inputs or outputs. Adding the state, as the current context, the module receives in the so-called calculators. This scheme allows the single module of the function to use in various modules of the calculators (Fig. 2).
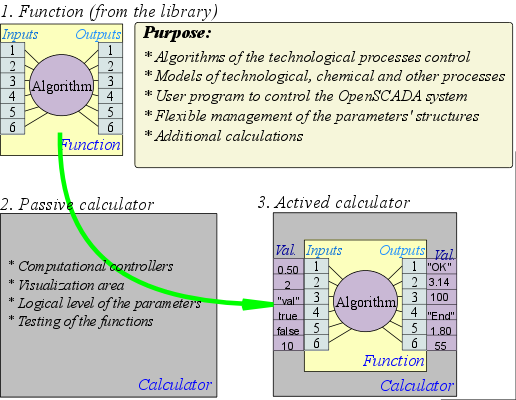
Fig. 2. The basis of the programming area of OpenSCADA system
4.3 Choosing the high-level language to implement the calculator on this language
To implement high-level language it is necessary to define the language to be used as the basis. Based on the principle that language must be sufficiently well-known and, if possible, be used by other projects as the internal language of calculation, lets examine the following languages: C, C++, Java, JavaScript and Phyton. Since C, C++, Java and JavaScript is practically came from the language C, we'll take into account the languages C++, Java and JavaScript. Language C++ is somewhat complicated, because it contains mechanisms to work with addresses and pointers. These opportunities are abundant for the tasks of the user programming area.
Lets stop on the languages of Java and JavaScript, which have simplified grammar. First, we'll implement the common grammar for Java and JavaScript with the further tendency to the language of JavaScript, since it is often used in other projects (Web-browser, KDE).
4.4 Designing the grammar of the parsers. Selecting a tool for creating syntactic and lexical analyzers
We know that to build a compiler or interpreter you need to create a lexical analyzer, parser and code generator or interpreter.
The lexical analyzer is constructed quite simply.
The parser is based on the concept of formal grammars and its creation - a nontrivial task. Therefore, there are ready-made tools to build a parser with the specified grammar. They include the parser's generator Yacc (AT&T and Berkeley). On the basis of this well-known parser generator many others are created, such as Bison and Zubr. All of them are compatible and can replace one another.
To develop the programming language the parsers' generator Bison was chosen, because it is distributed freely with almost all modern distributions of OS Linux, is developing and is multiplatform.
Any formal grammar can be written as:
G = <A, N, ã, P>
where :
N – nonterminal alphabet;
ã - axiom;
P – grammar rule.
Lets write the terminal and nonterminal alphabets:
A = {ERR, IF, ELSE, =, ADDEQ, SUBEQ, MULEQ, DIVEQ, FUNC, B_FUNC, B_FUNC1, B_FUNC2, VAR, CONST, ?, :, OR, AND, |, &, ^, >, <, GE, LE, EQ, NE, +, -, *, /, %, UN_MINUS, !, , ',', (, ), '{', '}', ; }
N = {root, solver, solve,assign, expr, prmlst, if, if_expr, end }
Description of the terminal alphabet is given in Table 1. Description of the nonterminal alphabet is given in Table 2. P grammar rules are given in Table 3. As the axioms of grammar it is defined: r = root;
Table 1: Terminal alphabet of the Java-like language (A)
| Terminal | Description |
| ERR | Error. Is injected by the lexical analyzer in case of an error in it. |
| error | Error. Terminates the job of parser. |
| IF | Keyword of the condition - “if”. |
| ELSE | Keyword of the condition - “else”. |
| = | Operation - to assign. |
| ADDEQ | Operation - “+=” |
| SUBEQ | Operation - “-=” |
| MULEQ | Operation - “*=” |
| DIVEQ | Operation - “/=” |
| FUNC | External function. |
| B_FUNC | Built-in function without parameters. |
| B_FUNC1 | Built-in function with one parameter. |
| B_FUNC2 | Built-in function with two parameters. |
| VAR | Variable, automatic variable, attribute of the system parameter or a function's parameter. |
| CONST | Constant. |
| ? | The first character of the operation “?:” |
| : | The second character of the operation “?:” |
| OR | Logical operation - “||” |
| AND | Logical operation - “&&” |
| | | Operation - bitwise OR |
| & | Operation - bitwise AND |
| ^ | Operation - exclusive OR |
| > | Operation - more. |
| < | Operation - less. |
| GE | Operation - more than or equal. |
| LE | Operation - less than or equal. |
| EQ | Operation - equivalent. |
| NE | Operation - not equivalent. |
| + | Operation - addition. |
| - | Operation - subtraction. |
| * | Operation - multiplication. |
| / | Operation - division. |
| % | Operation - the remainder in integer division. |
| UN_MINUS | Operation - unary minus. |
| ! | Operation - inversion. |
| ~ | Operation - bitwise inversion. |
| , | Separator (separates the parameters ôin functions). |
| ( | Select the priority in expressions and function's parameters. |
| ) | Select the priority in expressions and function's parameters. |
| { | Select the expressions block. |
| } | Select the expressions block. |
| ; | Completion of the expression. |
Table 2: Nonterminal alphabet of the Java-like language (N)
| Not terminal | Description |
| root | Root. All expressions must be turn to it. |
| solver | Solution. |
| solve | Element of the solution. |
| assign | Assignment. |
| expr | Expression. |
| prmlst | Function's parameters list. |
| if | Condition. |
| if_expr | Condition expression. |
| end | End of the condition or of the program. |
Table 3: Grammar of Java-like language
| Rule | Description |
| root: solver end | error | solution and end of the program; error. |
| solver: /*empty*/ | solver solve | empty solution; recursion of the solution. |
| solve: assign ';' | IF '(' expr ')' if solve end | IF '(' expr ')' if solve end ELSE solve end | FUNC '(' prmlst ')' ';' | '{' solver '}' | assignment; global short condition; global full condition; procedural call of the the outer function; blocks of code in brackets “{“ “}”. |
| assign: VAR '=' expr | VAR ADDEQ expr | VAR SUBEQ expr | VAR MULEQ expr | VAR DIVEQ expr | simple assignment; assignment with the addition; assignment with the subtraction; assignment with the multiplication; assignment with the division. |
| expr: CONST | VAR | VAR '=' expr | B_FUNC '(' ')' | B_FUNC1 '(' expr ')' | B_FUNC2 '(' expr ',' expr ')' | FUNC '(' prmlst ')' | expr '+' expr | expr '-' expr | expr '*' expr | expr '/' expr | expr '%' expr | expr '|' expr | expr '&' expr | expr '^' expr | '(' expr ')' | expr OR expr | expr AND expr | expr '<' expr | expr '>' expr | expr GE expr | expr LE expr | expr EQ expr | expr NE expr | '!' expr | '~' expr | '-' expr | expr if_expr expr end ':' expr end | constant; variable; assigning the variable inside an expression; built-in function without parameters; built-in function with one parameter; built-in function with two parameters; external function; addition; subtraction; multiplication; division; remainder of integer division; bitwise OR; bitwise AND; bitwise exclusive OR; brackets in the expression; logical OR; logical AND; less; more; more and equal; less and equal;; equal; not equal; logical negation; bitwise inversion; unary minus; condition within an expression; |
| prmlst: /*empty*/ | expr | prmlst ',' prmlst | empty list of parameters; expression as a parameter; list of parameters through “,”. |
| if: /*empty*/ | Start of the conditions (for condition's code generation). |
| if_expr: '?' | Start of the conditions inside the expression. |
| end: /*empty*/ | End of program or of the condition. |
Based on these rules we can construct a parser. However, the parser needs the lexical analyzer, which should perform an analysis of the stream of the input program, to allocate the lexemes and give them to the parser.
We'll make the lexical analyzer, which should perform the following functions:
- to determine the position of a character in the input stream and transfer it to the parser to report the position of errors;
- to process the comments;
- to control the end of the flow program stream;
- to allocate the numbers of four types: decimal, octal, hexadecimal and float;
- to allocate the strings;
- to allocate the symbols on the following priority list:
- key words;
- constants;
- built-in functions;
- external functions;
- already registered symbols of variables;
- new attributes of system parameters;
- new parameters of the function;
- new automatic variable.
- to allocate multicharacter lexemes, based on the terminal alphabet.
To simplify the language we'll use an implicit definition of local variables, which implies the definition of new variables, while giving it the first value. In addition, the type of local variable must be set in accordance with the type of value, which was firstly assigned to it. For example, the expression <Qr=Q0*Pi+0.01;> must define the variable type of variable Qr as the type of Q0.
In working with various types of data we'll user the mechanism of automatic casting in places where such casting has sense.
To comment the sections of code the characters «//» is provided. Everything that is after these characters until the end of the line should be ignored by the compiler (lexical analyzer).
Lets foresee that in the process of code generation of the virtual machine, compiler performs the optimization on the constants, and casts the constants' types to the desired one.
The optimizing on constant means the making of calculations on the two constants in the process of building the code and following pasting the result into the code. For example, the expression <y=pi*10;> should roll up to the simple assignment <y=31.4159;>.
The casting the constants' to the desired type is the formation the constant in the code, which eliminates the cast in the execution process. For example, the expression <y=x*10> in the case of a real type of variable <x>, must be transformed into <y=x*10.0>.
4.4.1 Elements of the language
As a result of the development there are implemented the following elements of programming language:
Key words: if, else, true, false.
Constants:
- decimal -- numbers 0–9 (12,111, 678);
- octal -- numbers 0–7 ( 012, 011, 076);
- hexadecimal -- numbers 0–9, letters a-f or A-F (0x12, 0XAB);
- real -- 345.23, 2.1e5, 3.4E-5, 3e6;
- boolean -- true, false;
- string -- “hello”.
Variables' types:
- integer -- -231...231;
- real -- 3.4 * 10308;
- boolean -- false, true;
- string -- up to 256 characters without switching to another line.
Built-in constants: pi = 3.14159265, e = 2.71828182.
Attributes of the system's parameters OpenSCADA.
Functions of the object model of the system OpenSCADA.
4.4.2 Operations
Operations, which will be supported by the programming language are presented in Table 4. The priority of operations is reduced from the top to the bottom. Operations with the same priority will be in one color group.
Table 4. Operations of the Java-like language
| Character | Description |
| () | Call of the function. |
| {} | Program blocks. |
| - | Unary minus. |
| ! | Logical negation. |
| ~ | Bitwise negation. |
| * | Multiplication. |
| / | Division. |
| % | The remainder of integer division. |
| + | Addition |
| - | Subtraction |
| > | More |
| >= | More or equal |
| < | Less |
| <= | Less or equal |
| == | Equal |
| != | Unequal |
| | | Bitwise "OR" |
| & | Bitwise "AND" |
| ^ | Bitwise "Exclusive OR" |
| && | Logical "AND" |
| || | Logical "OR" |
| ?: | Conditional operation (i=(i<0)?0:i;) |
| = | Assignmentå. |
| += | Assignment with the addition. |
| -= | Assignment with subtraction. |
| *= | Assignment with multiplication. |
| /= | Assignment with division. |
4.4.3 Built-in functions of the language
To provide high speed in mathematical calculations module provides built-in mathematical functions that are called on the instruction-level of the virtual machine. Built-in math functions:
- sin(x) - sinus x;
- cos(x) - cosineñ x;
- tan(x) - tangent x;
- sinh(x) - hyperbolic sine of x;
- cosh(x) - hyperbolic cosine of x;
- tanh(x) - hyperbolic tangent of x;
- asin(x) - arcsine of x;
- acos(x) - arc cosine of x;
- atan(x) -arc tangent of x;
- rand(x) -random number from 0 to x;
- lg(x) - common logarithm of x;
- ln(x) - natural logarithm of x;
- exp(x) - exponent of x;
- pow(x,y) - raising of x to the power y;
- sqrt(x) - square root of x;
- abs(x) - absolute value of x;
- sign(x) - sign of number x;
- ceil(x) - rounding of x to a greater integer;
- floor(x) - rounding of x to the lesser integer.
4.4.4 Operators of the language
The language supports two types of conditional operators. First - this is the conditional operator for use inside an expression, the second is the global one.
Conditional operator for use inside an expression based on the operations "?" and ":". As an example, we can write the following practical expression <st_open=(pos>=100)? True:false;>, which reads as "If the variable <pos> greater than or equal to 100, the variable <st_open> is set to "true", otherwise to "false".
The global condition is based on the keywords "if" and "else". As an example, the same expression, but otherwise <if(pos> 100) st_open = true; else st_open = false;>. As can be seen, it is recorded in the different way, but it reads equally.
4.4.5 Example of the program in Java-like language
Here are some examples of programs on the developed Java-like language:
//Model of the motion of the ball valve
if( !(st_close && !com) && !(st_open && com) )
{
tmp_up=(pos>0&&pos<100)?0:(tmp_up>0&&lst_com==com)?tmp_up-1./frq:t_up;
pos+=(tmp_up>0)?0:(100.*(com?1.:-1.))/(t_full*frq);
pos=(pos>100)?100:(pos<0)?0:pos;
st_open=(pos>=100)?true:false;
st_close=(pos<=0)?true:false;
lst_com=com;
}
//Valve model
Qr=Q0+Q0*Kpr*(Pi-1)+0.01;
Sr=(S_kl1*l_kl1+S_kl2*l_kl2)/100.;
Ftmp=(Pi>2.*Po)?Pi*pow(Q0*0.75/Ti,0.5):(Po>2.*Pi)?Po*pow(Q0*0.75/To,0.5):pow(abs(Q0*(pow(Pi,2)-pow(Po,2))/Ti),0.5);
Fi-=(Fi-7260.*Sr*sign(Pi-Po)*Ftmp)/(0.01*lo*frq);
Po+=0.27*(Fi-Fo)/(So*lo*Q0*frq);
Po=(Po<0)?0:(Po>100)?100:Po;
To+=(abs(Fi)*(Ti*pow(Po/Pi,0.02)-To)+(Fwind+1)*(Twind-To)/Riz)/(Ct*So*lo*Qr*frq);
4.5 Development of the internal virtual machine
The result of work of the parser with the lexical analyzer may be the directly interpretation (the program execution) or generation of the code inside the virtual machine.
Interpretation does not require additional efforts to develop the virtual machine and is a good solution in the case of not very demanding algorithms.
Virtual Machine allows you to implement high-performance computings by means of optimizing the code and exception of the superfluous analysis of lexical and syntactic analyzers, however, it requires considerable efforts to be developed.
As there is the paragraph in the development conditions, that requires providing of high-performance computings, then we'll stop on the development of the virtual machine.
There are many ways of constructing a virtual machine, one can note:
- stack machines;
- code based on quadruples.
Stack machines are the convenient way to build the virtual machine. The feature of the stack virtual machine is:
- operands of any operation are placed in the stack;
- an operation takes the operands from the stack, performs the action and puts the result in the stack;
- the following command is selected, and the cycle repeats.
The disadvantage of stack machines is that the stack is a dynamic structure to work with which a lot of time is spent on, in addition, to implement the memory for static figures in a separate computing session it must be provided the separate data structure.
Another class of virtual machines are virtual machines, based on the so-called quadruples. The essence of the quadruples is that the command consists of: <code> <result> <operand1> <operand2>
Where the result and the operands are references to registers of memory or structures. Code of the virtual machine of this class is somewhat more, but the structure of memory is static and can combine the functions of storage of static and dynamic calculations' data. Therefore, to build the virtual machine we'll choose the scheme based on quadruples.
All data in the virtual machine will be placed in registers. Register of the virtual machine must provide the structure that can store the following data:
- boolean values;
- integer values;
- real values;
- string values;
- reference to the function's parameter;
- references to the attributes of the parameters of the subsystem "DAQ".
Commands of the built virtual machine is given in Appendix A. The mechanism of the virtual machine's work will be as follows:
The parser allocates the commands and generates code in the semantic procedures of Bison. During the code generation virtual machine forms the list of registers. Registers, which contain references to the parameters of this function, attributes of parameters of the subsystem "DAQ" and internal variables, are to be initialized during code generation and no longer be used for other purposes. Other registers (dynamic data of the intermediate calculations) should be set aside and used for temporary purposes. Such registers are initiated by specific values at runtime of the program in the virtual machine. The resulting configuration of registers (the structure of memory) and the program code of virtual machine are used in the mode of calculating of the virtual machine. At the same time the configuration of registers does not change that allows to use of rapid mechanisms for access to registers and for the primary initialization of the registers' frame.
For addressing of the registers it used the one byte, which provides support for up to 255 parameters of the function (in the amount with internal variables).
4.6 Development of the block programming language
Languages of the block programming based on the concept of block diagrams. With that, depending on the nature of the block, block scheme can be: logic circuits, relay logic circuits, the model of technological process and more. The essence of the block scheme is that it contains the list of blocks and links between them.
From the formal point of view the block is an element which has inputs, outputs and an algorithm for computing. Based on the concept of the programming area and its basis (Fig. 2), block is the frame of parameters' values, associated with the function's object.
Of course, the inputs and outputs of blocks it is necessary to connect to get the whole block scheme. The following types of links will be provided:
- interblock - connecting the input of one block to the output of another, and also the input of one block to the input of another one;
- long interblock - connecting of the blocks of the controllers of the module;
- coefficients - the transformation of input into the constant, all inputs/outputs by default are initiated as the constants;
- external attribute of the parameter.
Ñonnections of blocks can be represented as links between the blocks as a whole (Fig. 3) or detail of the links (Fig. 4). In the process of binding the parameters of the blocks we will not adhere to strict compliance with types of parameters. This means that the parameters of different types can easily communicate with one another. And in the process of calculation it will be performed automatically casting.
Since the block calculator is based on the objects of the functions of an object model of the OpenSCADA system, then the parameter types of blocks are the same, that is: an integer, real, boolean and string.
Fig. 3. General links between the blocks of block scheme
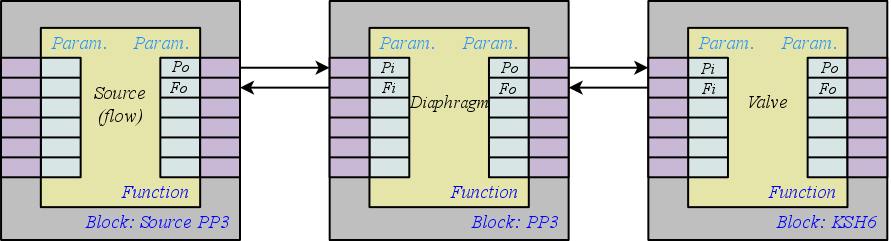
Fig. 4. Detailed links between blocks
4.7 Projecting of architecture
Based on the modular architecture of OpenSCADA system and reflections contained in the sections above, it was developed the following architecture of the programming area (Fig. 5).
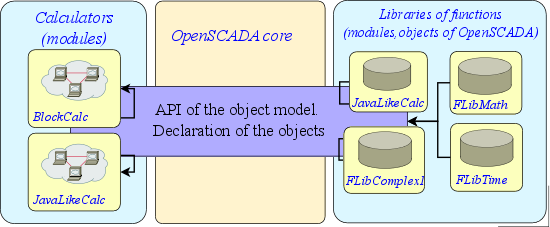
Fig. 5. The overall structure of the programming area
As you can see, the architecture of the programming area consists of three parts:
- API of the object model of OpenSCADA system with the declaration of basic objects;
- functions' libraries;
- calculating controllers.
This architecture of the programming area allows to distribute the process of creation and using. That is, the algorithms for computing in the form of functions' objects are provided by the one components, and are used for the calculations by the other ones.
In such a scheme there should be a layer that combines the components that provide algorithms with components that use them, which is especially important in the light of the fact that these components can be separated from the system, that is to by the modules. This layer should be the API of an object model of OpenSCADA system.
Based on the structure of the programming area, lets create classes of objects. Static class diagram with the separation of each component of the programming area is shown in Figure 6. Classes description is given in Table 5.
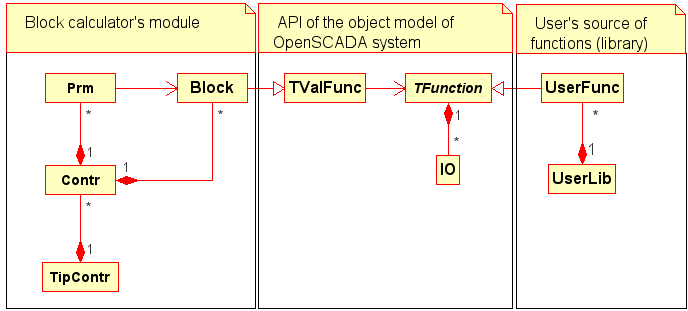
Fig. 6. Static class diagram of the programming area
Table 5. Classes of the programming area
| Class | Responsibility | Links |
| TFunction | The class of the function. It contains the description of the parameters (IO). In the ancestor it must include the implementation of the function's algorithm. | It is used be the calculators to associate it with the frame of values. It is the abstract, inherited by components that provide their own functions' libraries. |
| TValFunc | Class of the function's values. Contains the values of function in accordance with the composition of the parameters (IO) of the TFunction class. | It is aggregated with the object of the function TFunction for collaborative computing. It can inherited by classes of the calculator. An instance of the TValFunc class passed to the TFunction class during the computation to execute the algorithm in TFunction over the values in TValFunc. |
| IO | The class of the function's parameter. It contains the description of the parameter, its type and attributes. | It is used by the class of TValFunc values to determine the values of parameters. |
| UserLib | Class of the user's library . | It may provide the tool for creating user's functions. |
| UserFunc | Class of the user's functions. It provides the function's parameters and the computing algorithm. | It inherits the function's TFunction class. |
| Block | User's calculator class. It contains associated with the function TFunction frame of TValFunc values. It executes the process of calculating | It inherits the values frame class . |
4.7.1 Architecture of the calculator on the Java-like language
Based on the structure of the programming area (Fig. 5) and its class diagram (Fig. 6), we'll create classes of the calculator on the Java-like language (Fig. 7). Description of the classes is given in Table 6.
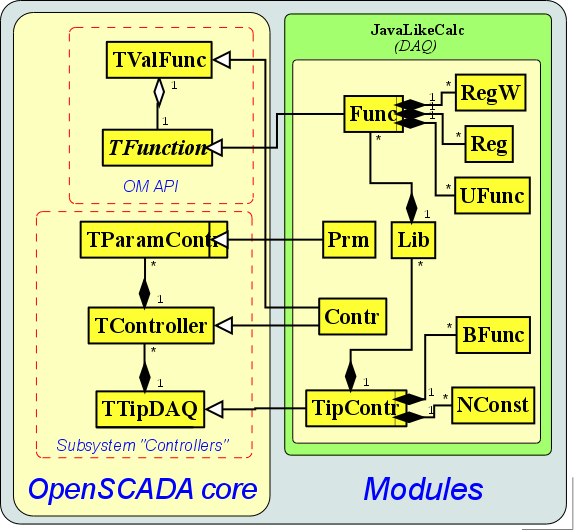
Fig. 7. The static class diagram of the module "JavaLikeCalc"
Table 6. Classes of the JavaLikeCalc module
In order to provide the directly calculation it must be provided the creation and linkage of the controller with the function of the same module. For the linkage with the function in the controller it is created the frame of values TValFunc, over which the periodic calculations are made.
To export the obtained values from the controller in the OpenSCADA system and to import values from the system to the controller the parameters of the controller of subsystem "DAQ" must be used. The parameters of the controller associated with the parameter of computing function (field of the data table) and must comply the reflection of values.
4.7.2 Architecture of the calculator of the block language
Based on the structure of the programming area (Fig. 5) and its class diagram (Fig. 6), lets create the classes of calculator on the blocks language (Fig. 8). Description of the classes is given in Table 7.
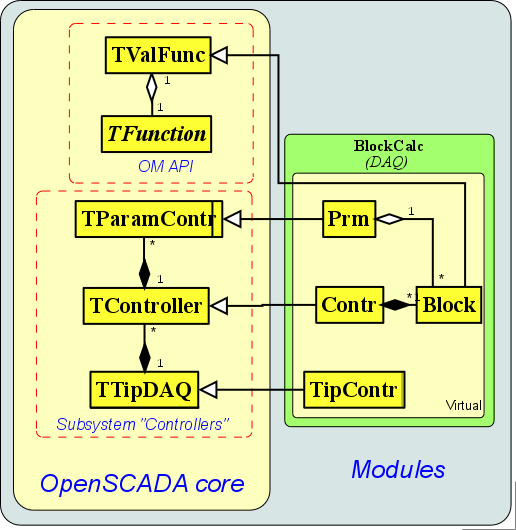
Fig. 8. The static class diagram of the module "BlockCalc"
Table 6. Classes of the BlockCalc module
| Class | Responsibility | Links |
| TipContr | Root class of the module, the main purpose of which is the access point into the module. | Inherits the class of the interface of the modules of subsystem 'Data sources' TTypeDAQ for integration into the OpenSCADA system. |
| Contr | The class of implementation of the controller. It contains the mechanism of periodic calculations over the algorithm of block scheme. | Inherits the controller's interface class TController. Contains the blocks of the block scheme. |
| Prm | The class of the implementation of parameter of subsystem "DAQ". It contains the mechanism of reflection of parameters of blocks of block scheme on the structure of parameter of the subsystem "DAQ" of OpenSCADA system. | Inherits the class of the interface of the parameter TParamSontr. It contains the links to the parameter of the block of block scheme. |
| Block | The class of the block. It contains the frame of values in accordance with the associated function. It contains the mechanism of links. | Inherits the class of the interface of values' frame TValFunc. It is referenced by the object of the parameter's class (Prm). Instances of the class of this type may contain links to one another. |
Each controller of this module contains the block scheme, which it should calculate in accordance with specified intervals.
The blocks in this case does not contain the structure of inputs/outputs (IO), but only contain the values based on the structure of the parameters of linked function. To connect with the block any functions of the object model (OM) of the OpenSCADA system can be used.
To provide an opportunity to export values from the block scheme to the OpenSCADA system lets envisage the possibility of reflecting the attributes of blocks on the parameters of the controller of the OpenSCADA system. Similarly, the values from the OpenSCADA system can get to the block scheme of the controller.
4.7.3 The standard architecture of libraries of the static functions
Based on the structure of the programming area (Fig. 5) and its class diagram (Fig. 6), lets create the architecture of classes for libraries of static functions (Fig. 9). Description of the classes is given in the Table 8.
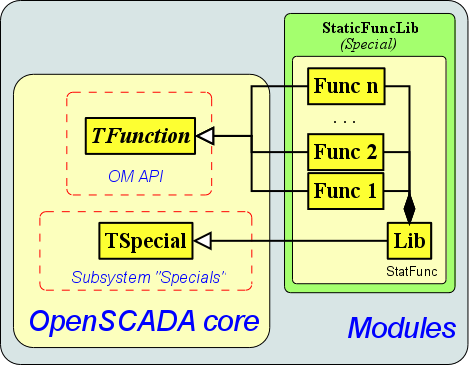
Fig. 9. The static class diagram of the static libraries of functions
Table 7. Classes of the static library of functions
| Class | Responsibility | Links |
| Lib | Root class of the module, the main purpose of which is the access point to the module. Serves as the library, and thus contains objects of static functions. | Inherits the class of the interface of modules of subsystem "Specials" TSpecial for integration into the OpenSCADA system. It contains the function objects. |
| Func | The class of functions. It contains the structure of parameters and the algorithm of their calculation. | Inherits the class of the interface of function TFunction. |
Based on this architecture there are constructed the following static libraries of functions:
- FLibComplex1 - the library of functions compatible with the SCADA Complex1 (Table 8);
- FLibMath - the library of standard mathematical functions (Table 9);
- FLibTime - the library of functions for working with time (Table 10);
Table 8. The function of the Complex1 library
| Id | Name | Description of the functions. Formulas of the functions' calculations |
| alarm | Alarm | The signal on the scale of the parameter:
out = if(val>max || val<min) then true; else false;
|
| cond < | Condition '<' | Condition '<' formula:
out=if(in1<(in2_1*in2_2*in2_3*in2_4)) |
| cond > | Condition '>' | Condition '>' formula:
out=if(in1>(in2_1*in2_2*in2_3*in2_4)) |
| cond_full | Full condition | Full condition formula:
out = if(in1<(in2_1*in2_2*in2_3*in2_4)) |
| digitBlock | Digit block | Set of digit signals. |
| div | Divider | Divider formula:
out = (in1_1*in1_2*in1_3*in1_4*in1_5 + in2_1*in2_2*in2_3*in2_4*in2_5 + in3) / |
| exp | Exponent | Exponent formula:
out=exp (in1_1*in1_2*in1_3*in1_4*in1_5 + (in2_1*in2_2*in2_3*in2_4*in2_5+in3) / |
| flow | Flow | Calculation of the flow formula:
f = K1*((K3+K4*x)^K2);
|
| increment | Increment | Increment formula:
out = if( in1 > in2 ) then in2 + in3*(in1-in2); |
| lag | Lag | Lag formula:
y = y - Klag*( y - x );
|
| mult | Simple multiplication | Simple multiplication formula:
out=(in1_1*in1_2*in1_3*in1_4*in1_5*in1_6)/ |
| multDiv | Multiplication + Division | Multiplication + Division formula:
out=in1_1*in1_2*in1_3*in1_4*in1_5* |
| pid | PID controller | PID controller |
| pow | Power | Power formula:
out=(in1_1*in1_2*in1_3*in1_4*in1_5)^ |
| select | Select | Select formula:
out = if( sel = 1 ) then in1_1*in1_2*in1_3*in1_4; |
| sum | Simple adder | Simple adder formula:
out=in1_1*in1_2+in2_1*in2_2+in3_1*in3_2+in4_1*in4_2 |
| sum_div | Sum with division | Sum with division formula:
out = in1_1*in1_2*(in1_3+in1_4/in1_5) + |
| sum_mult | Sum with multiplication | Sum with multiplication formula:
out = in1_1*in1_2*(in1_3*in1_4+in1_5) + |
Table 9. Standard mathematical functions
| Id | Name | Description |
| abs | Module | Math. function - module of the number. |
| acos | Arc cosine | Math. function - arc cosine. |
| asin | Arc sine | Math. function - arc sine. |
| atan | Arc tangent | Math. function - arc tangent. |
| ceil | Round to greater | Math. function - rounding to the greater integer. |
| cos | Cosine | Math. function - cosine. |
| cosh | Hyperbolic cosine | Math. function - hyperbolic cosine. |
| exp | Exponent | Math. function - exponent. |
| floor | Round to the lower | Math. function - rounding to the lower integer |
| if | Condition If | Function - condition "If". |
| lg | Common logarithm | Math. function - common logarithm. |
| ln | Natural logarithm | Math. function - natural logarithm. |
| pow | Power | Math. function - powering. |
| rand | Random number | Math. function - random number. |
| sin | Sine | Math. function - sine. |
| sinh | Hyperbolic sine | Math. function - hyperbolic sine. |
| sqrt | Square root | Math. function - square root. |
| tan | Tangent | Math. function - tangent. |
| tanh | Tangent hyperbolic | Math. function - tangent hyperbolic. |
Table 10. Time functions
| Id | Name | Description |
| date | Full data | Returns the full date of: second, minute, hour, day of the month, month, year, day of week, day of the year. |
| time | Full time (from 01.01.1970) | Returns the full time as the number of seconds since the epoch |
| ctime | Full time as a string | Returns the string of full-time "Wed Jun 30 21:49:08 1993". |
5. Implementation
Initial implementation of the programming area in the code was done using the obtained UML-model through the generation of C++ code in the program Umbrello. As the result, it was designed the object model interface (API) and components in the form of modules to the OpenSCADA system:
- “JavaLikeCalc” module of subsystem “DAQ”;
- “BlockCalc” module of subsystem “DAQ”;
- “FLibComplex1” module of subsystem “Specials”;
- “FLibMath” module of subsystem “Specials”;
- “FLibTime” module of subsystem “Specials”.
The general structure of all these components and API is shown in Figure 10.
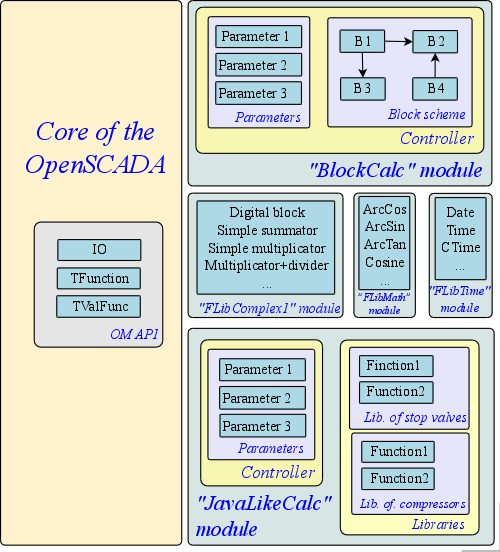
Fig. 10. The overall structure of the components of the programming area
Annex A. Commands of the internal virtual machine
Table. Commands of the internal virtual machine of the “JavaLikeCalc” module
| Command | Êîä | Description |
| End | 01 | The end of the program or conditional command. |
| MviB | 02 R V | Download the logical feature [V] in the register [R]. The initialization of the register. |
| MviI | 03 R V V V V | Download the integer [VVVV] to register [R]. The initialization of the register. |
| MviR | 04 R V V V V V V | ÇDownloading a real number [VVVVVV] to register [R]. The initialization of the register. |
| MviS | 05 R N S . . | Download the string [S. .] with the length [N] into the register [R]. The initialization of the register. |
| AssB | 06 R0 R1 | Assigning of the logical feature from the register [R1] to the register [R0]. |
| AssI | 07 R0 R1 | Assignment of the integer number from the register [R1] to the register [R0]. |
| AssR | 08 R0 R1 | Assigning of the real number from the register [R1] to the register [R0]. |
| AssS | 09 R0 R1 | Assigning of the string from the register [R1] to the register [R0]. |
| MovB | 0A R0 R1 | Moving the logical feature from the register [R1] to the register [R0]. The initialization of the register. |
| MovI | 0B R0 R1 | Moving the integer from the register [R1] to the register [R0]. The initialization of the register. |
| MovR | 0C R0 R1 | Moving the real from the register [R1] to the register [R0]. The initialization of the register. |
| MovS | 0D R0 R1 | Moving the string from the register [R1] to the register [R0]. The initialization of the register. |
| AddI | OE R0 R1 R2 | Addition of integers: R0 = R1 + R2. |
| AddR | OF R0 R1 R2 | Addition of reals: R0 = R1 + R2. |
| AddS | 1O R0 R1 R2 | Addition of strings: R0 = R1 + R2. |
| SubI | 11 R0 R1 R2 | Subtraction of integers: R0 = R1 - R2. |
| SubR | 12 R0 R1 R2 | Subtraction of reals: R0 = R1 - R2. |
| MultI | 13 R0 R1 R2 | Multiplication of integers: R0 = R1 * R2. |
| MultR | 14 R0 R1 R2 | Multiplication of reals: R0 = R1 * R2. |
| DivI | 15 R0 R1 R2 | Division of integers: R0 = R1 / R2. |
| DivR | 16 R0 R1 R2 | Division of reals: R0 = R1 / R2. |
| RstI | 17 R0 R1 R2 | Remainder of the integer division: R0 = R1 % R2. |
| BitOr | 18 R0 R1 R2 | Bitwise "OR": R0 = R1 | R2. |
| BitAnd | 19 R0 R1 R2 | Bitwise "AND": R0 = R1 & R2. |
| BitXor | 1A R0 R1 R2 | Bitwise exclusive "OR": R0 = R1 ^ R2. |
| LOr | 1B R0 R1 R2 | Boolean "OR": R0 = R1 || R2. |
| LAnd | 1C R0 R1 R2 | Boolean "AND": R0 = R1 && R2. |
| LTI | 1D R0 R1 R2 | Integer is less: R0 = R1 < R2. |
| LTR | 1E R0 R1 R2 | Real is less: R0 = R1 < R2. |
| GTI | 1F R0 R1 R2 | Integer is greater: R0 = R1 > R2. |
| GTR | 20 R0 R1 R2 | Real is greater: R0 = R1 > R2. |
| LEI | 21 R0 R1 R2 | Integer is less or equal: R0 = R1 <= R2. |
| LER | 22 R0 R1 R2 | Real is less or equal: R0 = R1 <= R2. |
| GEI | 23 R0 R1 R2 | Integer is greater or equal: R0 = R1 >= R2. |
| GER | 24 R0 R1 R2 | Real is greater or equal: R0 = R1 >= R2. |
| EQI | 25 R0 R1 R2 | Integer is equal: R0 = R1 == R2. |
| EQR | 26 R0 R1 R2 | Real is equal: R0 = R1 == R2. |
| EQS | 27 R0 R1 R2 | String is equal: R0 = R1 == R2. |
| NEI | 28 R0 R1 R2 | Integer is not equal: R0 = R1 != R2. |
| NER | 29 R0 R1 R2 | Real is not equal: R0 = R1 != R2. |
| NES | 2A R0 R1 R2 | String is not equal: R0 = R1 != R2. |
| Not | 2B R0 R1 | Denial: R0 = !R1. |
| BitNot | 2Ñ R0 R1 | Bitwise inversion: R0 = ~R1. |
| NegI | 2D R0 R1 | Inversion of the integer: R0 = -R1. |
| NegR | 2E R0 R1 | Inversion of real: R0 = -R1. |
| If | 2F R E E N N | The condition, if [R] is real, then the commands are executed after this operation and after the completion the transition is performed by the relative address [N N]; other the commands are executed by the relative address [EE] and in the end the transition to the relative address [NN] is done. |
| FSin | 30 R0 R1 | Sine function: R0 = sin(R1). |
| FCos | 31 R0 R1 | Cosine function: R0 = cos(R1). |
| FTan | 32 R0 R1 | Tangent function: R0 = tan(R1). |
| FSinh | 33 R0 R1 | Hyperbolic sine function: R0 = sinh(R1). |
| FCosh | 34 R0 R1 | Hyperbolic cosine function: R0 = cosh(R1). |
| FTanh | 35 R0 R1 | Hyperbolic tangent function: R0 = tanh(R1). |
| FAsin | 36 R0 R1 | Arcsine function: R0 = asin(R1). |
| FAcos | 37 R0 R1 | Arc cosine function: R0 = acos(R1). |
| FAtan | 38 R0 R1 | Arc tangent function: R0 = atan(R1). |
| FRand | 39 R0 R1 | Random number: R0 = rand(R1). |
| FLg | 3A R0 R1 | Common logarithm: R0 = lg(R1). |
| FLn | 3B R0 R1 | Natural logarithm: R0 = ln(R1). |
| FExp | 3Ñ R0 R1 | Exponent: R0 = exp(R1). |
| FPow | 3D R0 R1 R2 | Powering: R0 = pow(R1,R2). |
| FSqrt | 3E R0 R1 | Square-root: R0 = sqrt(R1). |
| FAbs | 3F R0 R1 | Modulus: R0 = |R1|. |
| FSign | 40 R0 R1 | Sign: R0 = sign(R1). |
| FCeil | 41 R0 R1 | Rounding to the greater: R0 = ceil(R1). |
| FFloor | 42 R0 R1 | Rounding to the less: R0 = floor(R1). |
| CProc | 43 F N R P P . . | The procedural call of the external function [F], with parameters [PP. .], in the number [N]. [R] - is not used. |
| CFunc | 44 F N R P P . . | Call of the external function [F], with parameters [PP. .], in the number [N]. The result of the function is placed in the [R]. |
Links